Tanxencias.

Enlace.

Inversión.

Definición.

Toda inversión depende dun punto chamado centro de inversión (O). Dous puntos alineados con dito centro son inversos ( A e A´) cando o produnto das súas distancias ao centro de inversión é unha cantidade constante ( k : potencia de inversión). Dito número será o mesmo para calquera punto que forme parte da mesma inversión.

K= OA. OA´

A potencia será positiva cando os puntos inversos se sitúen a un lado do centro de inversión.
A potencia será negativa cando o centro de inversión se sitúe no medio dos puntos inversos entre sí.

Imaxe.

O principal uso da inversión é a resolución de tanxencias.

Se dúas formas son tanxetes nun punto T a súas formas inversas serán tanxentes en T´, inverso de T.

A inversión manten as magnitudes dos ángulos. Se súas liñas se cortan formando un ángulo as súas rectas inversas formaran o mesmo ángulo.

Figuras dobles ou invariables na inversión.

- Unha recta que pase polo centro de inversión.
- Unha circunferencia de centro no centro de inversión e radio raíz cadrada de k.
- Circunferencia que pase a vez por dúas parellas de puntos inversos.


Inverso dun punto.

Coñecendo dous puntos inversos entre eles, o centro e un punto do que temos que obter o inverso.

Coñecendo o centro, un punto A e a razón k.

Fig 25.

Inverso dunha recta.

- Cando a recta pasa polo centro de inversión a súa inversa é ela mesma.

- Cando a recta non pasa polo centro de inversión.

Inverso dunha circunferencia.

- Cando no traxecto da circunferencia se sitúa o centro de inversión o seu inverso é unha recta.

- Cando o centro de inversión non pertence a circunferencia a súa inversa é outra circunferencia.

Exercicios.

Afinidade.

A afinidade é unha homoloxía cuxo vértice está ubicado no infinito ( punto impropio).

As parellas de puntos afines entre sí describen rectas paralelas. A dirección destas rectas paralelas é o que se denomina dirección de afinidade.

Carecen de rectas límite.

As formas afines poden estar colocadas a cada lado do eixe de afinidade ou nun único lado.

A simetría axial pode considerarse un caso particular de afinidade.



Exercicios.

Homoloxía.

Enlace.

Transformacións xeométricas.

Transformacións xeométricas no plano.

A) Isométricas.

A figura orixinal e a transformada conservan a forma e as medidas.

- Igualdade e identidade. Métodos.
- Traslación.
- Simetría. Central. Axial.
- Xiro.


B) Isomórficas.

A figura orixinal e a transformada manteñen as magnitudes dos seus ángulos e a lonxitude dos seus segmentos son proporcionais.

- Homotecia. Directa. Inversa. 
- Semellanza.
- Escalas.

C) Anamórficas.

A figura orixinal e a transformada non manteñen relaccións directas de medidas e ángulos.

- Equivalencia.
- Homoloxía.
- Afinidade.
- Inversión.

Curvas cónicas.

Enlace.

A elipse.
   
    Trazado a partir de diámetros conxugados.

A parábola.

A hipérbola.

Exercicios de repaso:

Elipse.

1) Constrúe un segmento AB que mida 54 mm. Sitúa o Foco F´ a unha distancia de 8 mm de B. Sendo AB o eixe maior da elipse determina o outro foco e o seu eixe menor.

2) Determina os eixes dunha elipse onde coñecemos os seus dous focos situados a unha distancia de 48 mm e un punto da elipse situado a 22mm de F e a 45mm de F´.

3) Traza unha elipse da que coñecemos un par dos seus diámetros conxugados, de lonxitudes 67 mm e 54 mm, sendo 75º o ángulo baixo o que se curtan.

4) Volve trazar a elipse empregando o método da caixa axonométrica.

Parábola.

1) Determina o Foco e o Vértice dunha parábola coñecendo un punto que pertence a mesma que dista 37 mm da directriz e 30 mm. do eixe.

Hipérbola

1) Dunha hipérbola equilátera coñecemos o eixe real onde están situados os seus dous vértices V e V´ a unha distancia de 5 cm. Determina as asíndotas e os focos da hipérbola.

2) Exercicio da proba da acceso a universidade dado a principio de curso. Opción B. Exercicio 1.

EXERCIOS de repaso sacados das probas de acceso a universidade.

Ejercicos de repaso de epvmanantiales


Intersección entre recta e elipse.





Intersección recta e parábola.






Intersección dunha recta cunha hipérbola.

Escalas.

Definición.

Enlace.

Escala gráfica.
Escala gráfica con contraescala.

A escala gráfica é unha regla onde representamos as divisións e subdivisións da escala que imos empregar. Permite aforrar tempo á hora de pasar as medidas ao debuxo.

1 Exercicio.
 Construe unha escala gráfica e contraescala de 5:1

Escala transversal o de décimas.

2 Exercicio:
Construe unha escala trasversal da escala 7:2

Triángulo uiversal de escalas.

Conversión de escala.

A representación numérica dunha escala pode cambiarse de fracción ordinaria a fracción decimal do seguinte xeito

E= 2:5
2/5= 0,4
Unidad de escala= 0,4
E=0,4

E ao contrario.

E= 0,5
E= 5/10
E= 1/2

Cuestionario.

Exercicio:

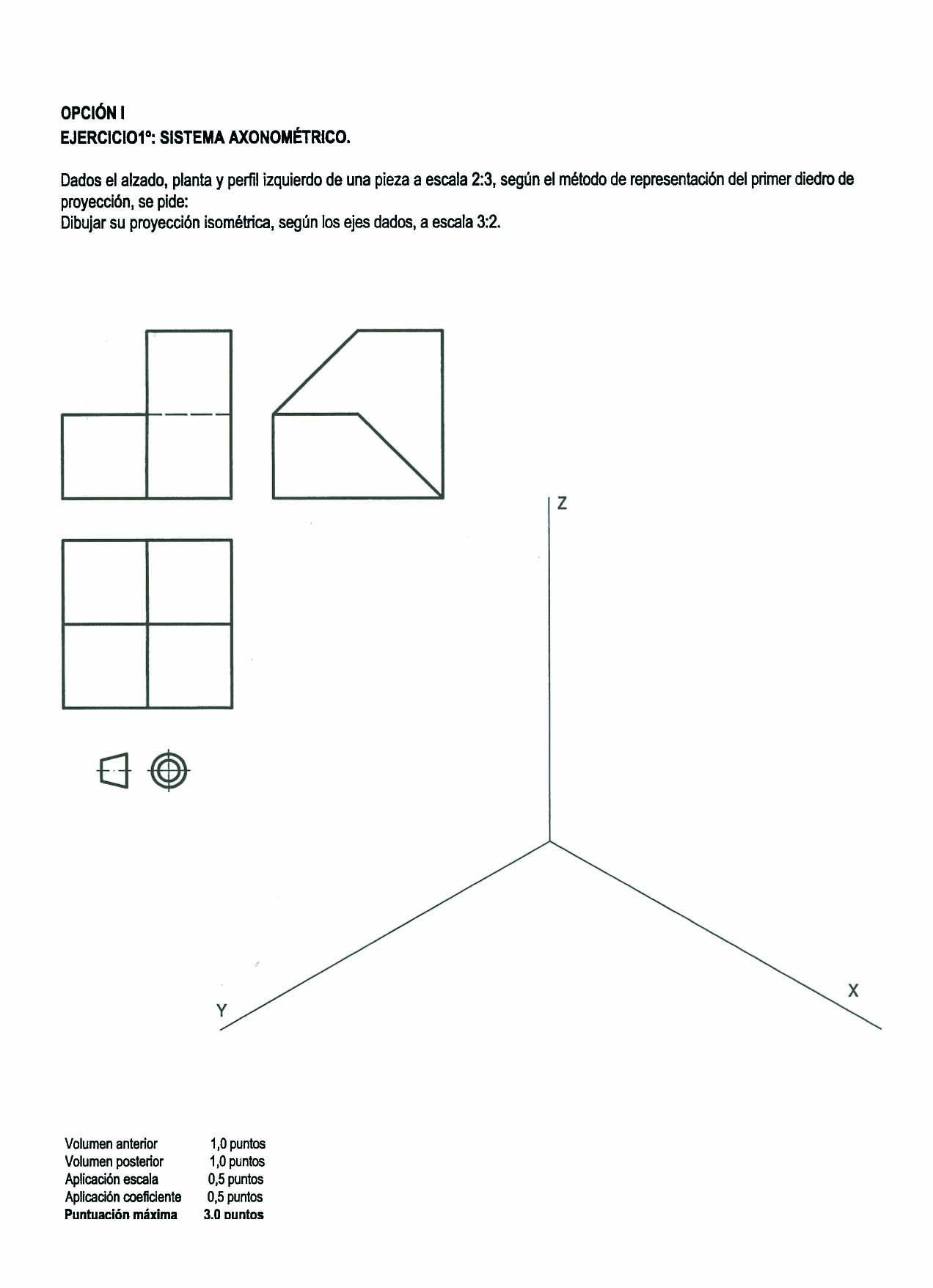
Dados alzado, planta e perfil dunha peza a escala 2:3, pídese debuxar a súa perspectiva isométrica a escala 2:1.

Imaxe.

Equivalencia e repaso de polígonos.

Definición.

Consideracións xerais.

Exercicios:

1) Debuxa un rectángulo equivalente a un triángulo cuxos lados midan AB= 55mm. BC= 40mm e AC=70mm.

2) Debuxa un rectángulo cuxo lado maior mida 40 mm e o menor 23 mm. Posteriormente obten o cadrado equivalente.

3) Traza un cuadrilátero equivalente a un pentágono regular de 45 mm de lado.

4) Volve debuxar un pentágono a partir dunha circunferencia de 70 mm de diámetro e obten un triángulo equivalente ao mesmo.

5) Debuxa un triángulo equivalente a un hexágono de 35 mm. de lado.

6) Traza o cadrado equivalente a unha circunferencia de 70 mm de diámetro.

7) Traza un cadrado equivalente a un triángulo rectángulo que teña como cateto menor un dado de 30mm e como medida de ángulo oposto a dito cateto un ángulo de 30º.

8) Dado o lado dun triángulo AB=45 mm e sabendo que o seu incentro está a 30 mm do vértice A e a 25 mm do vértice B. Traza o cadrado equivalente a dito triángulo.

*Puntos notables dun triángulo.

9) Debuxa un triángulo equilatero de 50 mm de lado e divideo en partes equivalentes.

10) Debuxa un cadrado de 30 mm de lado e a continuación traza outros tres cadrados de dobre, triple e cuatriple área.

...

Máis exercicios sobre equivalencias.

Arco capaz.

Definición.


Exercicios.

1) Arco capaz dun ángulo menor a 90º. (Alfa= 60º, segmento AB= 47mm).
2) Arco capaz dun ángulo maior de 90º. (Beta= 120º, segmento CD= 58mm).
3) Arco capaz dun ángulo recto. (Segmento LK=65mm).
4) Dados tres puntos A, B e C que non se encontran definindo unha liña recta encontra o punto onde visualizamos cada un dos extremos dos segmentos que definen os puntos baixo un ángulo de 45º.

Rectángulo áureo.

Definición.

O número de ouro.

Exemplo de aplicación do rectángulo áureo na arquitectura grega:
Imaxe templo grego.

Exemplo de utilización do rectángulo áureo en papelería:
Formatos DIN A-0 ...

Exercicios.

1) Construcción dun rectángulo áureo a partir do lado menor (35mm).
2) Construcción dun rectángulo áureo a partir do lado maior (50mm).
3) Construcción dunha espiral áurea a partir dun cadrado inicial de 10 cm de lado.

Curso 2017/2018.

Sombras en sistema axonométrico e perspectiva cónica. Centro propio e impropio.

Axonométrco. Centro impropio, no infinito.

Axonométrco. Centro propio, concreto.

Perspectiva cónica. Centro impropio, no infinito.

Perspectiva cónica. Centro propio, concreto.

Xeneralidades sobre acotación.

Enlace.
Tipos de acotación.

Práctica de perspectiva axonométrica trimétrica-

Coeficiente de reducción.
Exercicio.
A partir do debuxo dado en perspectiva isométrica fai a versión en dimétrica, trimétrica e caballera.

Exercicios de repaso.

1
2
3

Debuxa un cilindro en perpectiva isométrica de 10 cm de alto e 8 de diámetro de base.

2º Exercicio: 

- Debuxa un cono de 78 mm de alto con una base de 28 de radio a escala 4:3.

Triángulo universal de trazas e coeficiente de reducción en axonometría.

Como empregar escalas en perspectiva axonométrica.

Máis información.

Sistema axonométrico.

 

Perspectiva axonométrica de Agustín Camacho.

Perspectiva cónica.

Elementos.
Relacción entre a posición da peza e os puntos de fuga.

Exercicio1.
Exercicio2.

Exercicios de perspectiva cónica.

Exame.

Repaso diédrico.

1. Debuxa unha recta que conteña ao punto P.

        2. Debuxa un plano que conteña o punto P.

1. 

3. Debuxa dúas rectas que interseccionen nese punto P.
   
   
   
4. Traza posteriormente un plano que conteña a esas dúas rectas.
5.  Dada a seguinte recta traza dous planos que a conteñan e que intersecionen en dita recta.
   

6. Traza polo punto P unha recta paralela ao plano dado.

7. Traza polo punto P unha recta perpendicular ao plano.

8. Traza polo punto P unha recta de máxima inclinación (i) y máxima pendiente(p) do plano dado.

Repaso.

Enlace.

Distancia entre un punto e unha recta.

• Trazamos un plano auxiliar que conteña ao punto e que sexa perpendicular a recta.
• Determinamos a intersección entre o plano e a recta.
• A distancia en verdadeira magnitude do segmento PI é o resultado.

Traza un plano ( 45, 45º, 60º) e un punto P ( 80, 20, 30) e calcula a distancia en verdadeira magnitude entre ambos.

Distancia entre rectas paralelas.

Pasos:

• Trazar un plano perpendicular as dúas rectas.
• Determinar a intersección entre as rectas e o plano
• Obter a verdadeira magnitude da distancia que hai entre os dous puntos obtidos.
  

Exercicio:

Obten a distancia en verdadeira magnitude entre a recta r definida polos puntos A (20,13,10) e B (25,20, 15) e outra paralela a esta que pasa polo punto P (35, 10, 10).

Exercicios de repaso.

1. Obtén a intersección da recta definida polos puntos A (2,4,1) e B (7,1,4) e o plano  (2, 45º, 60º).
2. Representa unha recta que sexa paralela ao plano (15, 45º, 60º) e que pase polo punto P (19, -4, 6).
3. Representa o plano que sexa paralelo a (13,45º,60º) e que conteña ao punto P (19, 3, -3).
4. Obtén a distancia en verdadeira magnitude ente os planos paralelos (14,30º,45º) e (20, 30º, 45º).
5. Traza unha recta r perpendicular a un plano (10, 150º, 120º) de xeito que r conteña ao punto P (4,5,2). Obtén o punto onde r corta ao plano.

Distancia entre un punto e un plano.

Pasos:

1. Recta perpendicular ao plano alfa que pase por A.
2. Intersección entre a recta perpendicular e o plano.
3. Obter a distancia en verdadeira magnitude entre A e o punto de intersección I.

Intersección entre recta e plano.

Exercicio:

1. Obten a intersección entre a recta definida polo puntos A (6, -3, 3) e B (4,1,1) e o plano (12, 15º0, 135º).
2. Obten a intersección de la recta definida polos puntos A (2,4, 1) e B (7, 1, 4) có plano (2, 45º,60º)

Distancia entre dous puntos.

Exercicio. 

Debuxa os seguintes puntos e calcula a verdadeira distancia entre ambos.

A (3, 2, 1) 

B (2, 3, 0)

Posicións relativas entre planos.

• O elemento común a dous planos é unha recta. 
• Unha recta defínese coñecendo dous dos seus puntos. 
• Estos puntos veñen dados polas interseccións entre as trazas dos planos. 
• As intersección entre as dúas trazas verticais danos V2r e a intersección dentre as dúas trazas horizontais dos planos serve para obter H1r.

Exemplos:

- Plano oblicuo con plano horizontal.

- Plano oblicuo con plano vertical.

- Plano oblicuo con plano proxectante vertical.

- Intersección entre dous planos verticais.

Os planos paralelos son aqueles planos que teñen as súa trazas paralelas entre sí.

Un plano é perpendicular a outro cando contén unha recta perpendicular a dito plano. Unha recta é perpendicular a un plano cando a traza vertical do plano e perpendicular a r2 e traza horizontal do plano e perpendicular a r1.

Exercicios:

1) Obten a intersección dos seguintes planos dados. Alfa (1,30º,60º) e Beta (9, 105º, 135º).

2) Obten a recta intersección dos planos  (13, 90ª, 45º) e (22, 90º, 150º).

3) Obten a interesección entre os planos (13, 45º, 60º) e (infinito, -2, 4).

4) Traza el plano que contenga al punto P (18,1,2) y que sea paralelo a otro plano (23, 150º, 135º).

Posicións relativas entre rectas.

1) Rectas que se cortan.

Debuxa dúas rectas que se corten no punto P (6,6,8).

2) Rectas que se cruzan.

3) Retas paralelas.

Traza unha recta r que pase polos puntos A (3,2,1) e B (5, 2, 7) e a continuación traza unha recta paralela a r que pase polo punto C (8, -4, 2).

4) Rectas perpendiculares.

Traza una recta oblicua cualquiera y a continuación una perpendicular a la misma.

Vistas. Sistema diédrico.

Exercicio. Obten as vistas da seguinte peza en sistema europeo. 

• A peza ten 3 cm de ancho por 2.5 de profundidade. 
• A súa altura son 3 cm e cada escalón ten 1 cm dealtura con respecto a seguinte. 
• Os dous máis altos teñen unha dimensión en planta 1 cm de ancho por 1,25 de profundide.

Clase 4 dibujo tecnico Mod02. Sistema de representación Ortogonal de Zerojustice

Recta. Puntos de intersección cós bisectores.

Temos que localizar os puntos que pertencendo a recta teñen o mesmo valor na súa cota e no seu afastamento.

O máis sinxelo de obter é o punto de intersección có 2º bisector. É o punto onde interseccionan as súas proxeccións r1 e r2. Para obter o punto de interesección có primeiro bisector temos que facer unha liña auxiliar imitando ángulo que forma r1 ou r2 coa liña de terra.

Recta de máxima pendiente e de máxima inclinación.

Exame.

1)                 A partires das proxeccións dun punto A (5, 20, 15) sitúa as proxeccións doutro punto B sete unidades a súa dereita con 5 unidades menos de cota e 10 menos de afastamento. Onde está situado o punto B. Razoa a resposta. (0.75 puntos) (20%= 0.15).

O punto B está ubicado no 1º cuadrante, concretamente nun punto do 1º bisector. Debido a que ten cota e afastamento positivos có mesmo valor numérico.

2)                 Determina as trazas dunha recta m que pasa polos puntos A (7,12,7) e B (16,4,15) Fai un estudo da súa visibilidade. (1,5 puntos)

(20% = 0.3).

3)                 Indica as características e propiedades comúns dunha recta frontal e outra vertical. Axúdate dun debuxo a man alzada para as túas explicacións. (1 punto) (20% = 0.2).

4)                 Traza unha recta frontal que pase polo punto P (5,5,5) e forme un ángulo de 30º có ángulo vertical de proxección . Determina a súa traza propia e punto de intersección có segundo bisector, indicando o cuadrante ao que pertence. (1,5 puntos) (20% = 0.3).

5)                   Determina as proxeccións dun punto que tendo unha cota de 3 unidades pertence a un

 plano ೩ (4, 45º, 60º). (1,25 puntos) (20% = 0.25).